Homeへ

三角測量と一等三角点網
ここでは三角測量の方法と、日本地図の骨格ともいうべき一等三角点網について説明する。
○三角測量とは
三角関数の原理を利用して、距離を計測する方法を三角測量という。具体的には、正弦定理と余弦定理で、簡単に測量することができる。
	正弦定理（せいげんていり）
	正弦定理　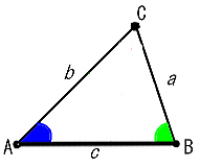　　　　　　　　　　　　　　　　○ １辺と２角が分かれば三角形を確定できる		三角形の内角の正弦（サイン）とその対辺には、次の関係が成り立つ。 　　　　 この定理を変形すると 　　　　 つまり、１辺（ｃ）と２角（ＡとＢ）が分かれば、辺（ａ）と辺（ｂ）を計算することができる。
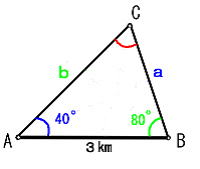			（計算例）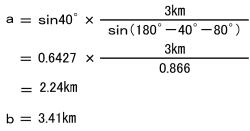
	余弦定理（よげんていり）
	余弦定理　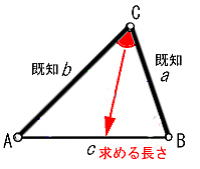　　　　　　　　　　　　　　　　○ ２辺と内角が分かれば三角形を確定できる		三角形の辺の長さと内角の余弦（コサイン）の間には、次の関係が成り立つ。 　　　　 　つまり、２辺（ａとｂ）とその内角（Ｃ）が分かれば、内角の余弦である辺（ｃ）を計算することができる。
○日本地図の骨組み（一等三角点網）
日本地区の作製にあたって、まず大まかな骨組が作られた。平均４５�qの一辺を持つ一等三角点網だ。
	基線と増大辺
	三角測量では、最初の１辺は実測しなければならないが、４５�qもの直線距離を実測することは不可能だ。また、正確な三角測量を行うには、正三角形に近い三角形が必要だ。そのため、実測可能な数�qの基線を設置し、そこから三角形を作り、組み合わせる方法（増大）により、数十�qの正確な距離を測量した。
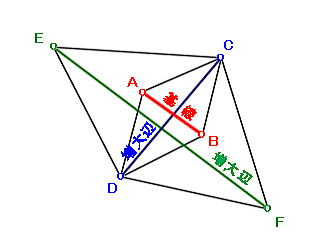			�@Ａ点とＢ点の間を実際に計測して基線ＡＢを作る。 �AＡ点とＢ点からＣ点を測量し、三角形ＡＢＣを確定する。 �BＡ点とＢ点からＤ点を測量し、三角形ＡＢＤを確定する。 �C２つの三角形を組み合わせ、三角形ＡＣＤを確定することで、増大辺ＤＣが求まる。 �DＣ点とＤ点からＥ点を測量し、三角形ＣＤＥを確定する。 �BＣ点とＤ点からＤ点を測量し、三角形ＣＤＦを確定する。 �C２つの三角形を組み合わせ、三角形ＣＥＦを確定することで、増大辺ＥＦが求まる。
	相模野基線
	１８８２年（明治15年）、日本で一番最初の基線が、相模原の下溝村と座間村に結ばれた。基線の長さは、5209.9697ｍだった。この基線から日本全国に三角点網が作られていった。 　相模野基線の場合は、３次まで三角形の増大が繰り返され、７６�qの正確な距離が測量された。

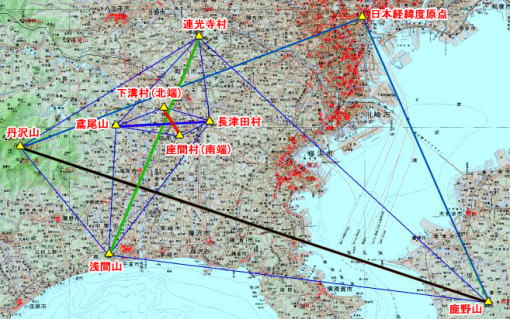相模野基線の増大 　�@下溝村（基線北端）設置 　�A座間村（基線南端）設置 　�B相模野基線（約５�q）実測 　�C鳶尾山（１次増大点）設置 　�D長津田村（１次増大点）設置 　�E１次増大辺（約１４�q）計算． 　�F連光寺村（２次増大点）設置 　�G浅間山（２次増大点）設置 　�H２次増大辺（約３７�q）計算 　�I丹沢山（３次増大辺）設置 　�J鹿野山（３次増大辺）設置 　�K３次増大辺（約７６�q）計算

	一等三角点網
	相模野基線に端を発した一等三角点網は日本全土に広まった。はじめ一等（本点）を約４５�q間隔で設置して大体の間隔を定め、ついで一等の補点（本点を含めて約２５�q間隔）の測量をして一等三角点網を完成させた。 　なお、基線は全国に１４か所設置され、そのれぞの網が重なる地点で誤差が調整された。

全国の基線 　�@相模野（神奈川県）　1882年． 　�A三方原（静岡県）　　 1883年 　�B饗庭野（滋賀県）　　 1885年 　�C西林村（徳島県）　　 1887年 　�D天神野（鳥取県）　　 1888年 　�E久留米（福岡県）　　 1889年 　�F笠野原（鹿児島県）　1892年 　�G塩野原（山形県）　　 1894年 　�H須坂（長野県）　　 　 1896年 　�I鶴児平（青森県）　　 1898年 　�J札幌（北海道）　 　　 1900年 　�K薫別（北海道）　　 　 1903年 　�L声問（北海道）　 　　 1908年 　�M沖縄（沖縄県）　 　　 1911年

日本地図の作成には一等三角点網は粗すぎるので、一等三角点を含めて約８�q間隔に二等三角点を設定し、以下二等三角点を含めて約４�q間隔に三等三角点を設け、更に以上を含めて約２�q間隔に四等三角点を設けて、各三角点から地形を２０mの等高線に描写して地形図が作成された。

	近畿の一等三角点網
			大阪周辺の一等三角点 　▲比良ヶ岳（滋賀県大津市） 　▲比叡山（滋賀県大津市） 　▲地蔵山（京都市右京区） 　▲鷲峰山（京都府宇治田原町） 　▲泉原山（大阪府茨木市） 　▲大浜公園（大阪府堺市） 　▲俎石山（大阪府岬町） 　▲葛城山（大阪府岸和田市） 　▲金剛山（奈良県） 　▲生駒山（奈良県生駒市） 　▲千丈寺山（兵庫県三田市） 　▲六甲山（神戸市北区） 　▲雄岡山（神戸市西区） 　▲釜口山（兵庫県淡路市） 　▲諭鶴羽山（兵庫県南あわじ市） 　▲友ヶ島（和歌山市加太） 　　　　▲：本点　　▲：補点

	三角測量の機材
	三角測量には、測量地点を示す三角点標石・盤石、角度を測定する経緯儀を用いる。ただ、数十�qもの先の測定をする場合、地面の三角点標石を見定めることができないので、覘標と呼ばれる測量櫓を建て、視界を妨げる木々を伐採しなければならなかった。
	三等経緯儀	覘標	カール・バンベルヒ三等経緯儀（けいいぎ） 　ドイツ製のこの三等経緯儀は最小読み取り角度が２秒で、水平角と高度角の両方が測定できた。新田次郎の小説「劒岳」で有名な柴崎芳太郎測量官が剱岳測量の際に用いた。 覘標（てんぴょう） 　覘標は観測の目標としての目印で、三角点標石上に建てられる櫓（やぐら）で、相手の三角点が見通せるよう二階建てのものもあり、ときには３０ｍもの高さにもなった。 運搬 　経緯儀は三角測量の中で最も重要な機器で、振動を与えてはいけないため常に人力で慎重に運搬された。運搬箱を含めた総重量は約60kgもあり、重い重い標石や盤石、そして覘標用の材木や食料などの運搬には、ヘリコプターやジープのない時代、相当苦労したようだ。
	経緯儀の運搬

Homeへ 　豆知識ﾒﾆｭｰへ 　次へ